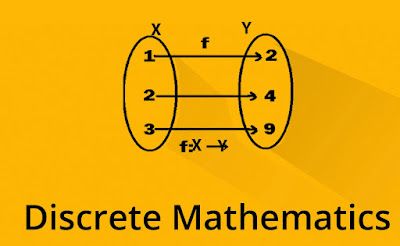
When we think of mathematics, continuous functions, calculus, or the complex beauty of infinity may come to mind. But there’s another branch that’s equally powerful and essential, especially in our digital age—discrete mathematics. Unlike continuous math, discrete math is concerned with finite or countable sets, focusing on topics like logic, combinatorics, graph theory, and algorithms. Despite its lesser-known reputation, discrete math is the backbone of computer science and crucial to modern-day technology. In this post, we’ll explore why discrete math matters and how it impacts various aspects of our lives.
What is Discrete Mathematics?
Discrete mathematics, at its core, deals with distinct and separate values—numbers, objects, or concepts that can be counted individually rather than existing on a continuous spectrum. This branch encompasses topics such as:
- Logic: The study of formal reasoning and the foundation of computer science.
- Set Theory: The study of collections of objects, crucial for understanding databases, probability, and more.
- Graph Theory: The study of nodes (vertices) and connections (edges) in networks, essential for networking, social media, and logistics.
- Combinatorics: The study of counting and arrangements, applied in data organization, optimization, and even DNA sequencing.
- Algorithms: Step-by-step procedures for solving problems, forming the basis of all computer programs.
Unlike calculus or continuous mathematics, which is about rates of change and curves, discrete math handles entities that are counted in whole numbers. This makes it foundational to computer science, where data is stored and processed in discrete chunks: bits, bytes, and binary numbers.
The Role of Discrete Math in Computer Science
Computer science as we know it would not exist without discrete mathematics. Every programming language, algorithm, data structure, and even the hardware itself is grounded in principles of discrete math. Here are a few key areas where discrete math has profound importance in computing:
- Logic and Boolean Algebra: Computers operate on binary systems—ones and zeros. Boolean algebra provides the rules and logic gates (like AND, OR, NOT) that dictate how these binary systems function, enabling all digital processing.
- Algorithms: At the heart of computer programming lies the algorithm, a sequence of instructions that allows us to solve problems efficiently. Algorithms are rooted in discrete math concepts, such as recursion, sorting, and searching, enabling computers to perform everything from simple calculations to complex tasks like image recognition.
- Graph Theory: Networks, whether they’re social, neural, or transportation-based, are modeled using graphs. Each user on a social network is a node, and the connections between them are edges. Algorithms based on graph theory help analyze these networks, detect trends, or even optimize traffic flows.
- Data Structures: Data storage and retrieval methods like trees, stacks, queues, and hash tables are fundamentally discrete structures. Understanding how these structures work and how they’re implemented in programming languages depends on discrete mathematics.
Without discrete math, advancements in computing and technology wouldn’t be possible. It’s the silent enabler behind everything digital, from smartphones and the internet to artificial intelligence and cryptography.
Cryptography: Protecting Data with Discrete Math
In an age where privacy and security are paramount, cryptography—a subset of discrete math—has become crucial. Cryptography is the science of encoding and decoding messages, and it relies heavily on number theory, particularly the properties of prime numbers.
For instance, RSA encryption, one of the most widely used encryption techniques, is based on the difficulty of factoring large numbers into primes. It’s easy to multiply two large primes, but computationally challenging to reverse the process and determine the original factors without significant computing power. This difficulty protects sensitive information like credit card details and personal data from hackers.
Discrete math also powers public-key cryptography, which allows secure communication over the internet without needing to share a secret key. By using discrete math concepts like modular arithmetic and prime numbers, cryptography makes secure e-commerce, online banking, and confidential communications possible.
Optimizing Real-World Processes with Combinatorics and Graph Theory
Discrete math isn’t just an abstract science; it has practical applications in optimizing processes and decision-making. Let’s consider two examples: combinatorics in scheduling and graph theory in logistics.
- Combinatorics and Scheduling: Combinatorics, the study of counting and arranging, helps solve scheduling problems where resources need to be allocated efficiently. Imagine organizing a tournament with multiple teams and games, or scheduling employees in a shift-based job. Combinatorics provides formulas and methods to calculate possible arrangements, ensuring resources are used optimally and conflicts are minimized.
- Graph Theory in Logistics: Logistics companies use graph theory to optimize routes and reduce costs. Each delivery location is a node, and routes between them are edges. Algorithms like Dijkstra’s (for finding the shortest path) and the Traveling Salesman Problem (for minimizing travel cost) help companies determine the best routes for their fleets. This is crucial for industries that rely on large-scale distribution networks, such as Amazon and FedEx.
These applications show how discrete math helps solve complex real-world problems, making processes more efficient and cost-effective.
Artificial Intelligence and Machine Learning
Artificial intelligence (AI) and machine learning (ML) rely on mathematical models that include discrete structures. From decision trees to neural networks, discrete math concepts help organize data, recognize patterns, and make predictions.
- Decision Trees: These are algorithms that categorize data points based on their attributes, often represented as branching structures. Decision trees are foundational in ML because they help in classification and prediction tasks, where clear-cut “yes or no” decisions are needed.
- Neural Networks: Although neural networks are inspired by continuous functions, they are structured in discrete layers, with each neuron represented by a node. Graph theory helps model these networks, and discrete structures make their design and implementation feasible in computer algorithms.
- Pattern Recognition: AI and ML models often rely on combinatorics to manage and analyze large datasets. The models generate multiple combinations of features to detect the best pattern, improving the accuracy and reliability of predictions.
Thus, discrete math provides tools that are integral to the development of AI and machine learning, shaping the future of technology and innovation.
Enhancing Logical and Analytical Thinking
Beyond specific applications, discrete math sharpens our logical and analytical skills. By working with precise definitions and logical statements, students and professionals alike learn to approach problems methodically, analyze potential solutions, and verify outcomes.
For instance:
- Logical Proofs: Learning to create proofs, especially in logic, helps train the mind to break down complex problems into manageable parts and analyze their truthfulness.
- Problem Decomposition: In programming, large problems are divided into smaller, manageable parts, a practice rooted in the principles of discrete math.
- Algorithmic Thinking: Understanding how to develop algorithms to solve problems promotes critical thinking and efficiency.
These skills are valuable not only in technical fields but also in everyday decision-making, where logical and strategic thinking play a role.
Conclusion
Discrete mathematics may not always receive the spotlight, but its influence on the digital world is undeniable. From powering the fundamental operations of computers to securing data through cryptography and optimizing real-world logistics, discrete math is a key enabler of modern technology. It shapes industries, advances research, and enhances the ways we interact with the world through logical reasoning and efficient problem-solving.
As technology continues to evolve, the importance of discrete math will only grow. So whether you’re a student, a tech enthusiast, or someone interested in how things work, understanding discrete mathematics opens the door to a world of innovation and possibility. Embracing discrete math is not just a journey through numbers and logic—it’s an essential step toward shaping the future.